Part 4 – The Power Cross & Advanced Conversion Charts
In part 1, part 2 and part 3 of this tutorial series, you learned all about how lenses work, why prescriptions for glasses are sometimes different than prescriptions for contact lenses, and how to calculate a contact lens prescription from a prescription for glasses.
In this 4th and final part, I will explain the power cross technique for converting a glasses prescription to contact lenses. This technique is taught to optometrists, opticians, optometric assistants, para-optometric technicians, etc to help them work through complicated conversions.
I am not a doctor. The information provided on this page is for general educational purposes only. You are not receiving medical advice or being prescribed contact lenses on this page. Please read Contacts Advice Terms of Use before continuing.
The Power Cross
As the name implies, this technique involves drawing a cross. You will be drawing a different power cross for each eye.
Let’s work with the following prescription:
| Sphere | Cylinder | Axis | |
| Right | -4.25 | -1.00 | 020 |
| Left | -5.00 | -1.50 | 160 |
Right Eye
Drawing the reference lines
Start by drawing two perpendicular lines of equal length. It should look like this.
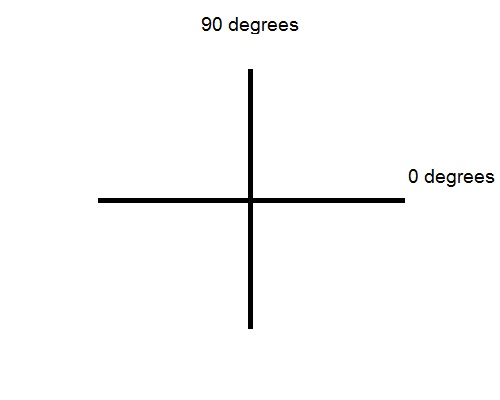
These are just going to be reference lines. They represent 0 degrees and 90 degrees.
Drawing the power lines
Next you will draw two more perpendicular lines of equal length over top of the reference lines you just drew. These lines will represent the two principal powers on the glasses prescription.
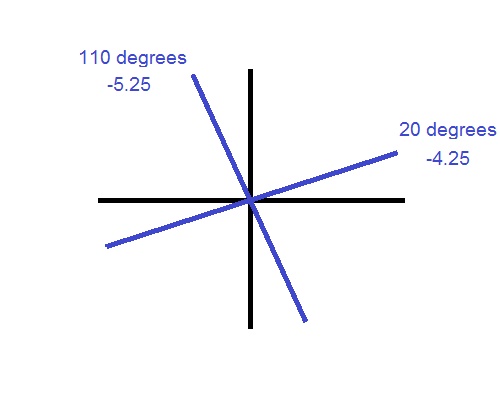
Before you draw them, take a look at the axis on the glasses prescription. In this case it is 20. Estimate 20 degrees along the reference cross and draw your first line there.
Draw your second line perpendicular to the one you just drew. In this case, it will be at 110 degrees.
Note: You can use a protractor if you want to be perfectly exact with your angles and lines, but a general estimate is all that’s really needed.
Identifying the powers
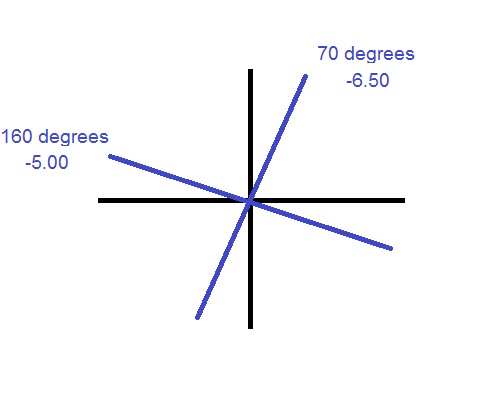
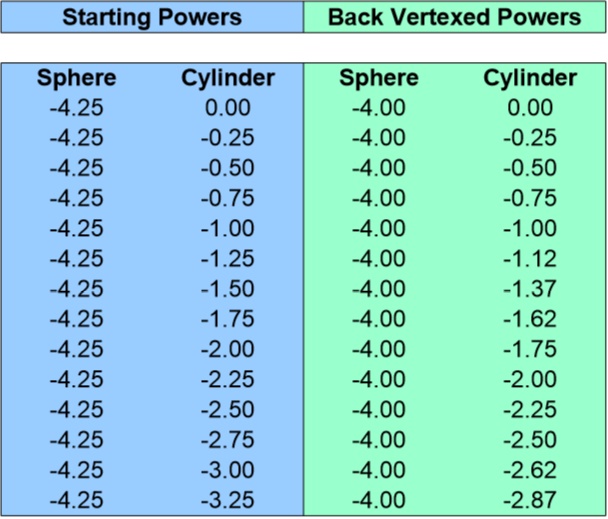
The line that you drew in the direction of the axis (20 degrees) is your first principle power and it has the same power as the ‘Sphere’ number. So go ahead and write the power down beside the line. In the case of our example, it is -4.25.
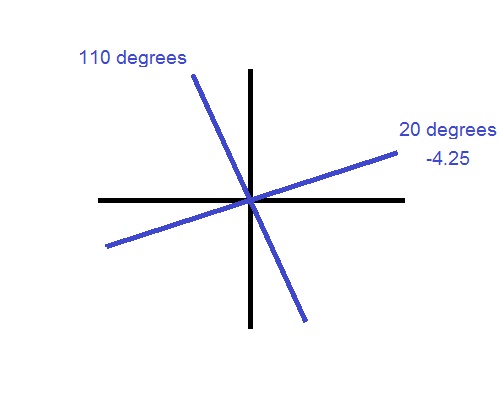
The line that you drew 90 degrees off (110 degrees) of the principle power line is the second principle power. Now if you remember from parts 2 and 3, the second principle power is not the ‘Cylinder’ number. It is the ‘Cylinder’ number PLUS the ‘Sphere’ number. In this example it is:
-4.25 + -1.00 = -5.25
So go ahead and write down the second principle power beside the second principle power line.
You have now drawn a graphical representation of the glasses prescription.
Back vertexing each power
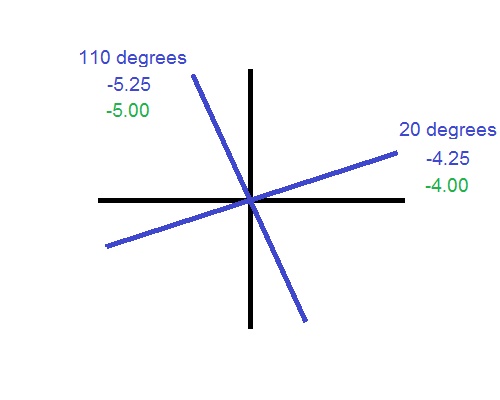
Using you favorite Vertexing Conversion Chart, look up the power for both of your principle powers and write down the converted power next the original power. If you’re not familiar with how to use a Vertex Conversion Chart, read parts 1 and 2 of this tutorial series.
 |
 |
Once you have converted the principle powers, you have before you a graphical representation of the contact lens prescription. All that’s left is to write it down in prescription form (called negative cylinder format).
Returning to prescription form
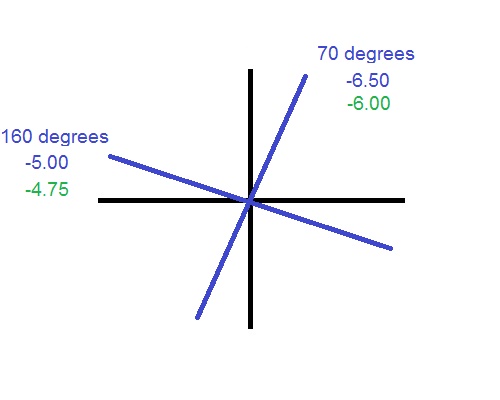
The ‘Sphere’ for the contact lens prescription will be the converted power from the line you drew in the direction of the axis. In this case, it is -4.00.
The ‘Cylinder’ number for the contact lens prescription is not simply the other power you converted. It is going to be the difference between the converted power of the second principle power and the converted power of the first principle power. In this case it is…
-5.00 – -4.00 = -1.00
Then we put the ‘Sphere’, ‘Cylinder’ and ‘Axis’ numbers together. The final contact lens numbers for the right eye would be:
| Sphere | Cylinder | Axis | |
| Right | -4.00 | -1.00 | 020 |
A power cross diagram does not change the axis. Ideally, the axis for a contact lens prescription would be identical to the axis in the glasses prescription. However, due to restrictions int he availability of different axis in contact lenses, sometimes it has to be rounded either up or down. Review part 3 of this tutorial for more information on how to do that.
For the left eye
Drawing the power lines
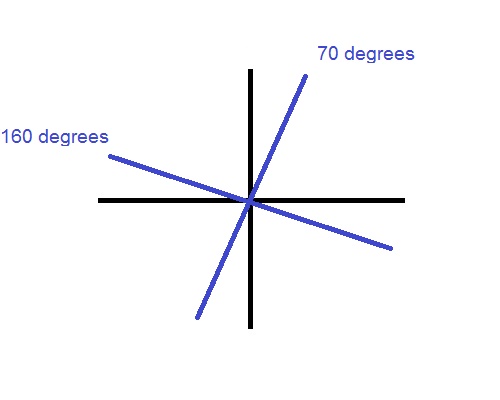
Identifying the powers
Back vertexing each power
 |
 |
Returning to prescription form
| Sphere | Cylinder | Axis | |
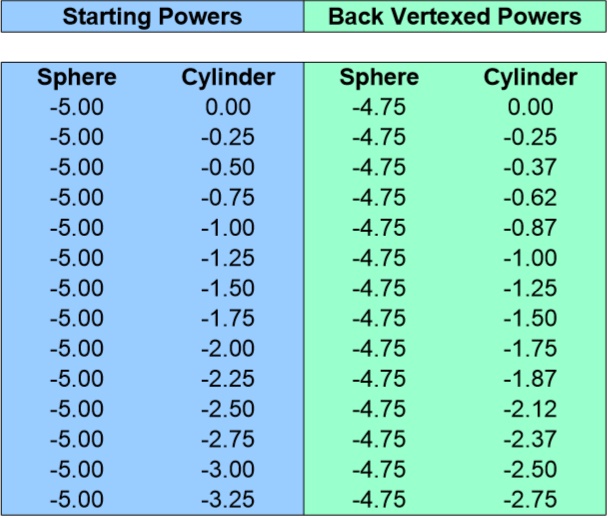
| Left | -4.75 | -1.25 | 160 |
Final contact lens prescription
We’ve now used a the power cross technique to convert the prescription for glasses for both the right and left eyes to contact lenses. The final contact lens prescription would be:
| Sphere | Cylinder | Axis | |
| Right | -4.00 | -1.00 | 020 |
| Left | -4.75 | -1.25 | 160 |
Converting Prescriptions the Easy Way
You’ve now learned a couple of different ways of converting glasses prescriptions to contact lenses. Each of them involves adding and subtracting positive and negative numbers, and looking up numbers on a chart. It can be easy to lose track of things while you’re doing these calculations, which is why the power cross is handy; it keeps everything clear and organized. But the downside is that it takes time.
Fortunately, there is an easier and faster way to go about it. There are now charts that you can use that don’t just convert 1 number at time, but 2. That means that you can look up your ‘Sphere’ and ‘Cylinder’ values at the same time, find their converted values, and all without ever having to do a single calculation or draw a power cross.
These charts were developed right here at Contacts Advice and they are called Vertex Conversion Charts for Sphere and Cylinder. They cover all prescriptions in the following ranges:
Sphere 0.00 to -8.00
Cylinder 0.00 to -3.25
If the numbers on the prescription you are trying to convert falls within the ranges above, you can use Contacts Advice’s Vertex Conversion Charts for Sphere and Cylinder to get the converted contact lens numbers in a fraction of a second.
How to use the charts
Let’s use the prescription in the example above to see how these charts are used. The prescription was:
| Sphere | Cylinder | Axis | |
| Right | -4.25 | -1.00 | 020 |
| Left | -5.00 | -1.50 | 160 |
For the right eye, the ‘Sphere’ is -4.25 and the ‘Cylinder’ is -1.00. You simply pull up the -4.25 ‘Sphere’ chart and find -1.00 in the ‘Cylinder’ column. As you can see from the chart below, the numbers in the green section are the same as the numbers we calculated using the power cross method (but this was A LOT faster).
For the left eye, the ‘Sphere’ is -5.00 and the ‘Cylinder’ is -1.50. You simply pull up the -5.00 ‘Sphere’ chart and find -1.50 in the ‘Cylinder’ column. As you can see from the chart below, the numbers in the green section are the same as the numbers we calculated using the power cross method (but this was A LOT faster).
The charts are free to the public. To gain access to them, you require only to sign up for Contacts Advice’s monthly deals newsletter which alerts you of all the best online glasses and contact lens deals once a month.




10 Responses
Susan Neighbors
I dont understand how to use charts. the eyeglass prescription is:
RT: sphere +0.50 cylinder SPH axis blank dist PD 30.5
LT: sphere +1.25 cylinder -0.25 axis 060 dist PD 29.5
How can I convert this for contact lenses?
Thanks
Julie
Hi Susan,
I apologize about the charts. The reason why you probably had difficulty using them is because I only made them to cover prescriptions that are nearsighted (sphere numbers that are negative). Your prescription is farsighted (sphere numbers that are positive).
If we were to apply the same formula to your numbers, we would get:
R: sphere +0.50
L: sphere +1.25
Now of course this is not an official prescription for contact lenses. Only your eye doctor can prescribe you contact lenses. The processes explained in my tutorial series just explains how they go about doing it :)
Jade
Hello.
I read all of your articles and attempted to convert my contact lens prescription to glasses. My rx for contacts are:
OD: -5.50
OS:-4.00
I do not have any astigmatism. So far, I’ve gotten OD=-4.00 and OS=-5.88 for glasses. Did I do this correctly?
Julie
Hi Jade,
I think you may have made a mistake somewhere…
When you take a -5.50 and back vertex it (using the chart), you get -5.12.
When you take a -4.00 and back vertex, you get -3.87.
Contact lenses are not available in -5.12 so that has to be round to either -5.00 or -5.25. Your eye doctor usually shows you both to see which one works better for you.
Contact lenses are also not available in -3.87. Usually, eye doctors will keep this at -4.00, but it could also be brought down to -3.75 if they think that would be better for you.
I hope this helped you with your calculations. Please remember that this website does not provide medical advice and you are not being prescribed anything here.
James
Thank you
Julie
You’re welcome.
Cheers :)
Linda
Hi Julie
I was today at an eye doctor but I was not really satisfied, because as I saw it he was rather in a haste to get done with my examination and in the end I was really worried about my prescription. It seemed to me so unprofessional. That’s why I tried to google it and see if I can prove it for myself. My glasses prescription is:
OD sph:+3.5 cyl: +1.0 acis:90
OS sph:+3.5 cyl: +1.0 acis:95
And underneath this he wrote just “lenses +4.00”
I am so sorry that I am asking you this after you explained everything. Please tell me what you think because I have to determine if I will go to another doctor for another examination or not, and honestly I don’t want to because it’s costing me.
Thank you so much :)
Julie
From what I’m seeing his conversion seems sensical. Of course by ‘lenses’ he means contact lenses.
Richard
Thank you for putting all that information in a clear and understandable format.
Julie
You’re welcome :)